题目链接
题目描述
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
输入描述:
1 | 题目保证输入的数组中没有的相同的数字数据范围: 对于%50的数据,size<=10^4 对于%75的数据,size<=10^5 对于%100的数据,size<=2*10^5 |
示例1
输入
1 | 1,2,3,4,5,6,7,0 |
输出
1 | 7 |
解题思路(by others)
基于归并排序的分治策略,以数组 {7, 5, 6, 4} 为例。
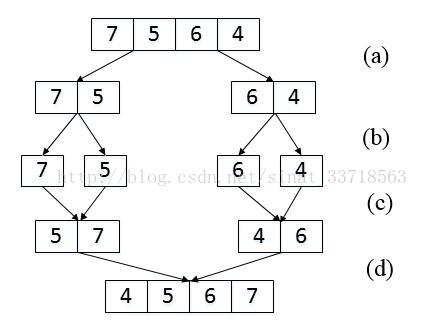
- 把长度为 4 的数组分解成两个长度为 2 的数组
- 把长度为 2 的数组分解成两个长度为 1 的数组
- 将 4 个长度为 1 的子数组归为两个长度为 2 的数组,即将长度为 1 的子数组合并,并统计逆序对
- 归并时,两个指针 p 和 q 分别指向两个子数组的末端(p 指向左子数组的末端,q 指向右子数组的末端)。如果 p 指向的值大于 q 指向的值,那么 p 与 q 及 右子数组中 q 前的值均构成逆序对
- 将两个长度为 2 的子数组归为长度为 4 的数组,即将长度为 1 的子数组合并,并统计逆序对
具体解法如下:
1 | class Solution { |