剑指offer：变态跳台阶

题目链接

NowCoder

题目描述

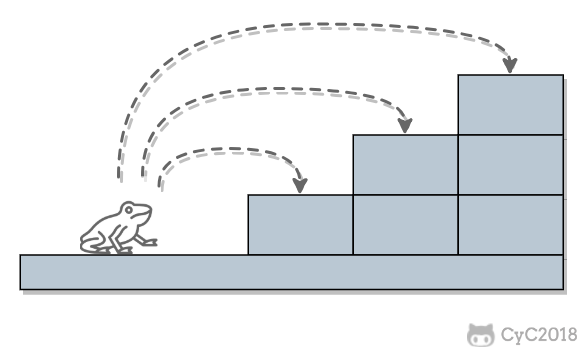
一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级… 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法

解题思路 （by myself）

跳上 n 级台阶，第一次跳可以跳 1级、2级…、n级

• 如果第一次跳 1 级，则剩下 n - 1级，问题变成跳上 n - 1级有几种跳法？
• 如果第一次跳 2 级，则剩下 n - 2级，问题变成跳上 n - 2 级有几种跳法？
• ……
• 如果第一次跳 n 级，则剩下 0 级，问题变成跳上 0 级有几种跳法？（虽然跳上0级只有0种跳法，但是第一次跳 n 级，第二次跳 0 级算作一种跳法，所以 f(0) = 1）

显然，第一次跳法有 n 种，剩下 n - i 级（i 为第一次跳楼梯的级数）。

通过上述这种分析，我们可以把这个问题转换为递归问题来完成。

我的解法如下：

class Solution {
public:
    int jumpFloorII(int number) {
        if  (number == 0 || number == 1) return 1;
        int ans = 0;
        for (int i = 1; i <= number; i++) {
            ans += jumpFloorII(number - i);
        }
        return ans;
    }
};

解题思路（by others）

跳上 n-1 级台阶，可以从 n-2 级跳 1 级上去，也可以从 n-3 级跳 2 级上去…，那么

f(n-1) = f(n-2) + f(n-3) + ... + f(0)

同样，跳上 n 级台阶，可以从 n-1 级跳 1 级上去，也可以从 n-2 级跳 2 级上去… ，那么

f(n) = f(n-1) + f(n-2) + ... + f(0)

综上可得

f(n) - f(n-1) = f(n-1)

即

f(n) = 2*f(n-1)

所以 f(n) 是一个等比数列

具体解法如下：

class Solution {
public:
    int jumpFloorII(int number) {
        int ans = 1;
        for (int i = 1; i < number; i++) ans *= 2;
        return ans;
    }
};