红黑树

考研数据结构并没有涉及红黑树，所以在这里整理一下。

红黑树的特性

红黑树是指满足以下性质的二叉搜索树（BST，binary search tree）：

• 每个结点为黑色或红色
• 根结点为黑色
• 每个叶子结点（实际上是NULL指针）为黑色
• 不能有两个相邻的红色结点。如果一个结点是红色，那么它的两个子结点都是黑色
• 对于每个结点，从该结点到其所有子孙结点的路径中包含的黑色结点数量必须相同（平衡性）

解释：

• 黑色高度：从根节点到叶子节点的路径中包含的黑色节点数。性质 4 保证了从根节点到叶子节点的最长路径的长度不会超过任何其他路径的两倍。因为黑色高度相同，在每个相邻的黑色结点中至多再插入一个红色结点。

  假如有一棵黑色高度为 3 的红黑树：从根节点到叶节点的最短路径长度是 2，该路径上全是黑色节点（黑节点 – 黑节点 – 黑节点）。最长路径也只可能为 4，在每个黑色节点之间插入一个红色节点（黑节点 – 红节点 – 黑节点 – 红节点 – 黑节点），性质 4 保证绝不可能插入更多的红色节点。

• 红黑树的最长路径是一条红黑交替的路径

• 对于给定的黑色高度为 N 的红黑树，从根到叶子节点的最短路径长度为 N-1，最长路径长度为 2 * (N-1)。红黑树通过这种限制来保证它的大致平衡。

红黑树和AVL树的比较

1. 红黑树不追求”完全平衡”，即不像AVL那样要求节点的左右子树的高度差不超过1，它只要求部分达到平衡。
2. 红黑是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决
3. 删除节点导致失衡，AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而RB-Tree最多只需要旋转3次实现复衡
4. 由于AVL更加平衡，AVL的查找效率更高
5. 红黑树是功能、性能、空间开销的折中结果

红黑树的插入

按照二叉搜索树的方法找到插入位置，因为红黑树有颜色约束，所以在插入新结点后要进行颜色调整。

具体步骤如下：

1. 根节点为NULL：直接插入新节点并将其颜色置为黑色
2. 根节点不为NULL：
   • 找到要插入新节点的位置
   • 插入新节点
   • 更新调整颜色

插入结点默认颜色为红色。如果默认结点为黑色，因为红黑树每条路径的黑色节点数目相同，所以调整起来非常繁琐。插入红节点不需要调整其他路径，如果它的父亲为黑，那么直接插入，如果他的父亲为红那么在该路径上面开始分情况调整。

具体的调整过程有三种情况：

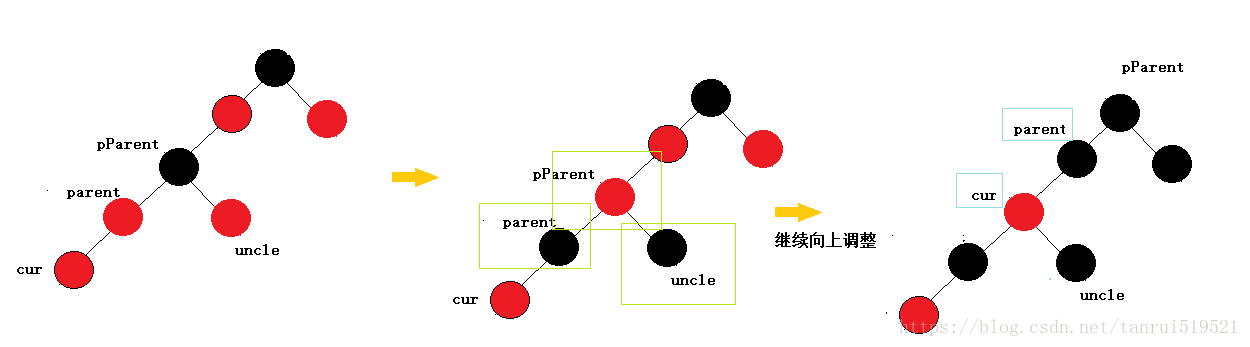
1. cur为红，parent为红，pParent为黑，uncle存在且为红，则将parent,uncle改为黑，pParent改为红，然后把pParent当成cur，继续向上调整。

   

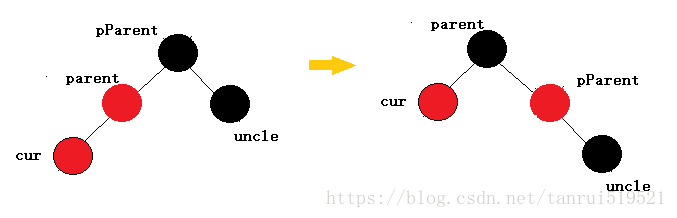
2. cur为红，parent为红，pParent为黑，uncle不存在或为黑， parent为pParent的左孩子，cur为parent的左孩子，则进行右单旋转

   uncle不存在：

   

   uncle存在且为黑：

   

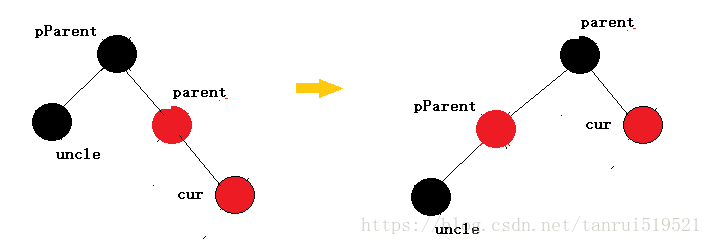
   如果parent为pParent的右孩子，cur为parent的右孩子，则进行左单旋转

   uncle不存在：

   

   uncle存在且为黑：

   

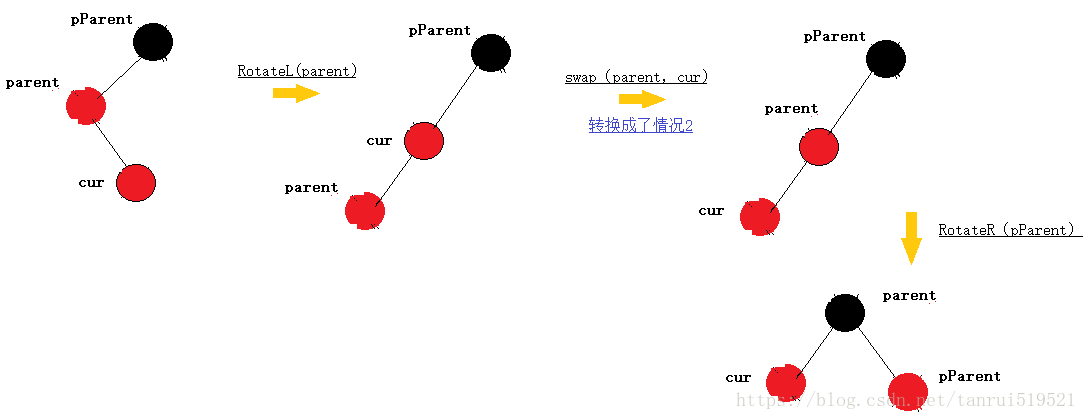
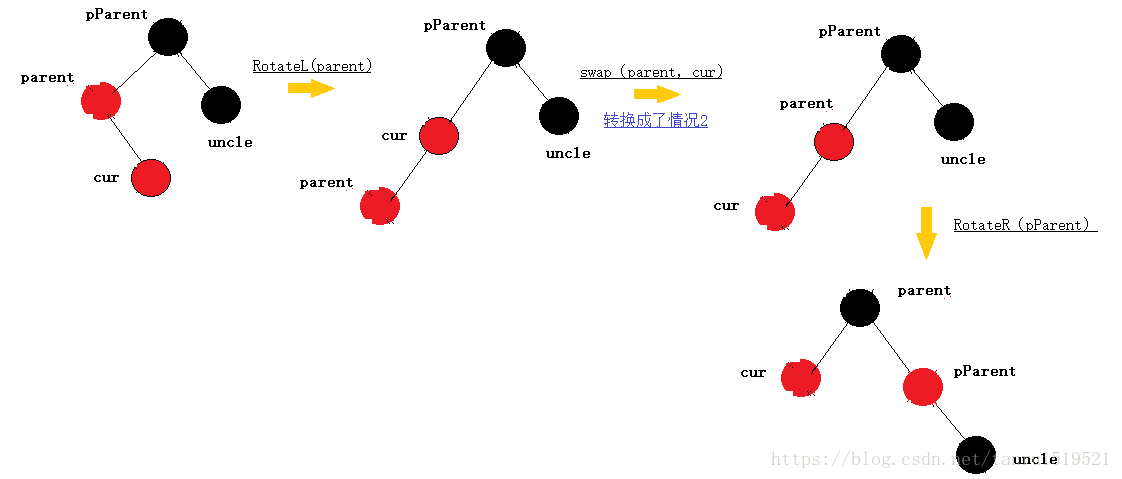
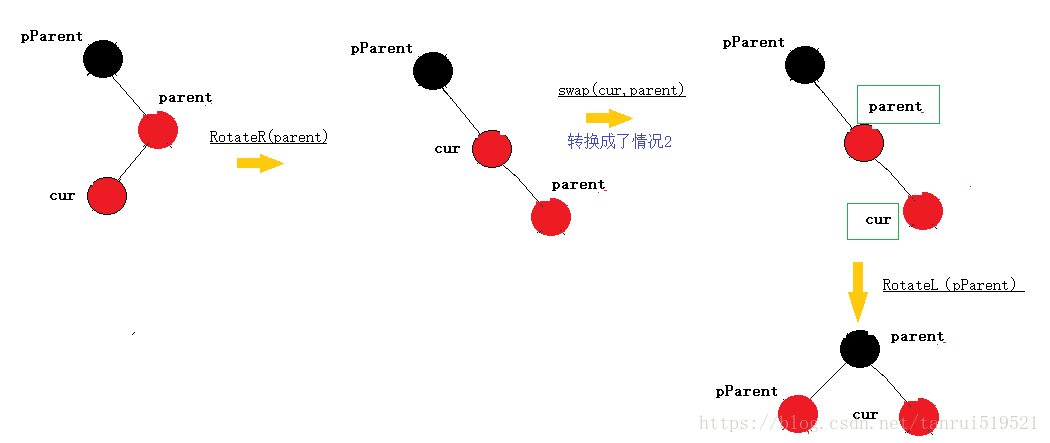
3. cur为红，parent为红，pParent为黑，uncle不存在或为黑，parent为pParent的左孩子，cur为parent的右孩子，则针对p做左单旋转

   uncle不存在：

   

   uncle存在且为黑：

   

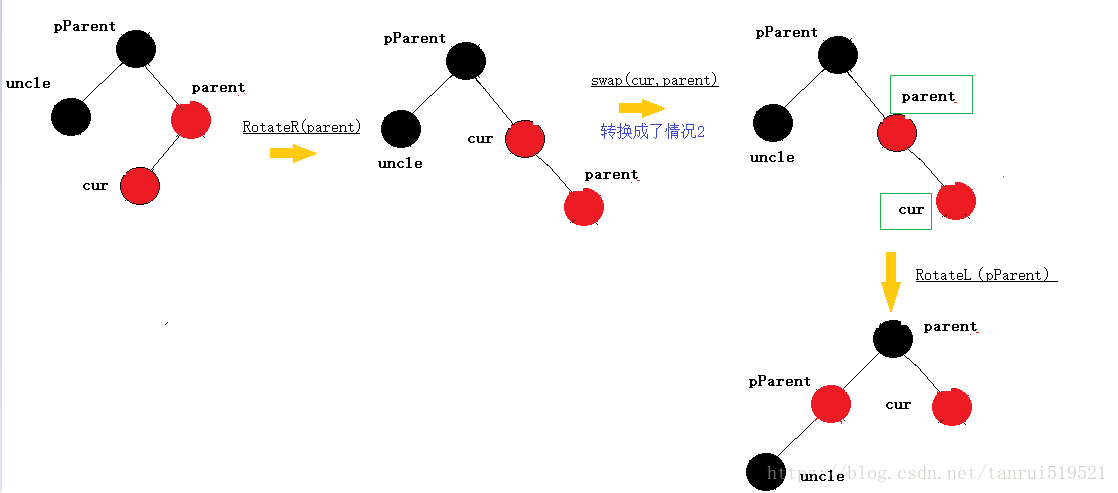
   如果parent为pParent的右孩子，cur为parent的左孩子，则针对parent做右单旋转

   uncle不存在：

   

   uncle存在且为黑：

   

红黑树的删除